基于占空比模糊控制的光伏发电系统MPPT技术
本文摘要: 文中以两级式光伏并网发电系统为研究对象,建立了任意外界环境下的光伏阵列数学模型。由于光伏阵列的非线性输出特性,将模糊控制思想引入...
文中以两级式光伏并网发电系统为研究对象,建立了任意外界环境下的光伏阵列数学模型。由于光伏阵列的非线性输出特性,将模糊控制思想引入最大功率点跟踪,提出占空比模糊控制的扰动观察法的MPPT控制策略,并通过计算机进行仿真验证。太阳能作为一种巨量的可再生能源,是近期急需的能源补充,又是未来能源结构的基础,开发利用太阳能具有重大的战略意义。所有光伏发电系统都希望$太阳能光伏阵列在同样日照、温度的条件下尽可能大的输出电能,因此在理论和实践上提出了太阳能光伏阵列的最大功率点跟踪(MPPT)问题。
目前实现MPPT的方法有恒定电压(CVT)法,扰动观察(P&O)法及增量电导(INC)法等。文中研究$光伏发电系统中的MPPT问题,基于模糊控制理论,即利用模糊集合的基本概念和连续隶属度函数的理论,提出了占空比模糊控制干扰观察法。通过MATLAB/Simulink建模仿真,实现在任意外界环境下最大功率点的跟踪,并与非模糊控制的占空比干扰观察法相比较,结果表明该方法在快速性和稳定性方面取得了更好的效果。
1 光伏电池的数学建模
光伏电池模型通常要求仅采用厂家提供标准条件(光照强度Sref=1000W/m2,电池温度Tref=25℃)下的光伏电池板测试参数Isc、Uoc、Im、Um,并且要在满足工程精度的情况下尽可能地简化模型。
简化的光伏电池的数学模型为:
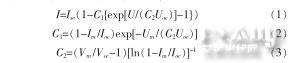
式中,Isc为标准条件下光伏电池的短路电流;Uoc为标准条件下光伏电池的开路电压;Im为标准条件下光伏电池的最大功率点电流;Um为标准条件下光伏电池的最大功率点电压。因此,只要知道这4个参数,就可以得到在标准条件下的光伏电池I—V特性曲线。
假定$光伏电池特性曲线基本形状不变,根据标准条件下的Isc、Uoc、Im、Um和任意的光照强度、环境温度等参数,可以计算出任意外部环境下的Isc’、Uoc’、Im’和Um’,得到光伏电池模型:
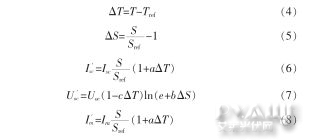
 2 占空比模糊控制实现MPPT
2 占空比模糊控制实现MPPT
2.1 算法原理
基于占空比扰动观察法原理,目标量为:光伏阵列的输出功率P;控制量为:Boost电路的占空比D。
根据功率值变化量△P(n)=P(n)-P(n-1)和n-1时刻的占空比调整步长△D(n-1),决定当前时刻的调整步长大小△D(n)。光伏发电系统的模糊控制原理图如图1所示。
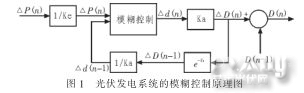
图1中,输入△P(n)表示第n时刻与前一时刻输出功率差的实际值,△p(n)表示△P(n)对应于模糊集论域中的值;输入△D(n-1)表示第n-1时刻占空比D调整步长的实际值,△d(n-1)表示△D(n-1)对应于模糊集论域中的值。输出△D(n)表示第n时刻占空比D调整步长的实际值,△d(n)表示△D(n)对应于模糊集论域中的值;D(n-1)表示第n-1时刻占空比的实际值,D(n)表示第n时刻占空比的实际值.e-Ts为一个单位延迟环节,Ke、Ka分别表示功率差和调整步长的量化因子。
在每一次寻优周期开始时,采样当前时刻的输出功率值P(n)和前一时刻调整步长△D(n-1),计算当前时刻P(n)和前一时刻P(n-1)的差值△P(n),并对△P(n)和△D(n-1)进行量化,得到模糊集论域中的变量△p(n)和△d(n-1),将其作为$模糊控制器的输入,通过模糊推理得到当前时刻的调整步长△d(n),经重心法反模糊化后,得到控制量占空比调整步长△D(n)的实际值,再与当前时刻的占空比D(n-1)相加得到下一时刻的占空比D(n),调整光伏阵列的输出电压和功率,然后就进入下一次的寻优周期。不断重复上述过程,直到输出功率差△P(n)达到精度要求,即,到达了光伏系统的最大功率点。
2.2 算法实现
2.2.1 确定输入和输出变量的模糊子集及论域
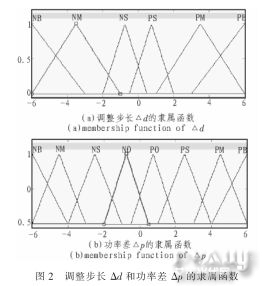
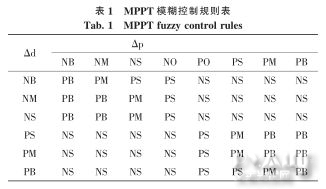
将语言变量分别定义为8个和6个模糊子集,即△p={NB,NM,NS,NO,PO,PS,PM,PB};△d={NB,NM,NS,PS,PM,PB}。其中:NB,NM,NS,NO,PO,PS,PM,PB分别表示负大,负中,负小,负零,正零,正小,正中,正大等模糊概念。并将论域规定为13个等级,即:△p={-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6};△d={-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6}。
2.2.2 确定隶属函数
选择常用的三角形隶属函数,占空比调整步长△d和功率差△p的隶属度函数分别如图2所示。
2.2.3 模糊决策表
根据占空比扰动观察法的原理,当前时刻的占空比调整步长△D(n)是由功率差△P和前一时刻的占空比调整步长△D(n-1)的变化量决定的。依据光伏阵列P-V特性曲线的分析,并考虑外界环境因素对光伏阵列输出特性的影响,得到以下调整占空比步长△D(n-1)的原则:
1)如果输出功率增加了,则继续按原来步长方向调整,否则,向相反方向调整;
2)在最大功率点附近时,采用较小的调整步长,减少跟踪时的功率损失;离最大功率点较远时,采用较大的调整步长,以加快跟踪速度。
3)当温度和光照强度等外界因素突然变化使得光伏阵列的输出功率发生较大变化时,系统能迅速地作出反应。
遵循上述原则,应用If A and B then C的模糊规则,模糊规则表如表1所示。
2.2.4 反糊方法
在模糊控制编辑器中,模糊推理采用成熟且容易成功实现的Mamdani推理法,“交”方法为min,“并”方法为max,推理方法为min,聚类方法为max,反模糊方法选择具有较高精度的重心法,如图3所示。
3 仿真分析
外界环境条件为:光照强度S=1 000 W/m2,环境温度T=25℃。负载阻值R=50 Ω。量化因子:Ka=0.005,Ke=2.0。采用固定步长为0.001,仿真器设置为ode3,运行时间为1 s。得到功率P和占空比D变化波形如图4所示。
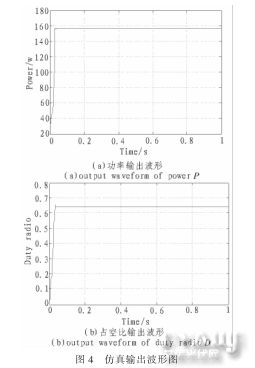
从图4(a)的输出功率仿真波形可以得知:在Pm=157.3W,Dm=0.638,t=0.039 s左右,光伏阵列就工作在最大功率点,实现了最大功率点跟踪,并且功率波形平衡光滑,几乎没有振荡。仿真结果表明了$模糊控制方法可以使光伏系统快速平稳地跟踪到最大功率点。
模拟外界环境变化,光照强度在1 s时由800 W/m2变为1 000 W/m2,环境温度在2 s时由25℃变为0℃,仿真时间为3 s,其他仿真参数设置不变,仿真得到的功率和占空比波形如图5所示;图6为相同外界条件下,非模糊控制占空比扰动观察法功率和占空比的输出波形。
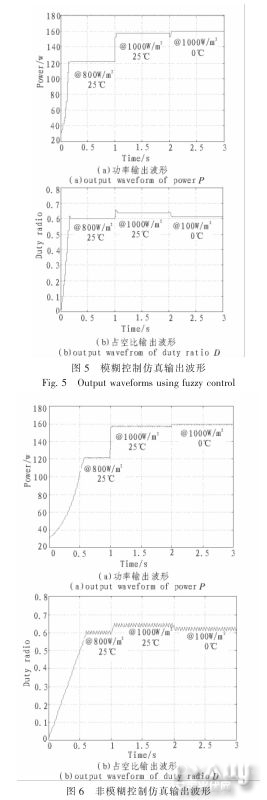
由图5和图6可以看出,当光照强度为1 000 W/m2,环境温度为25℃时,采用模糊控制法,系统在0.18 s就跟踪上了最大功率点,达到了稳定,而采用非模糊控制,系统在0.55 s才跟踪上最大功率点;当外界环境发生变化时,模糊控制法能够快速跟踪到新的最大功率点,波形到达稳态,没有剧烈振荡,而非模糊控制法达到稳定时出现了剧烈的振荡。通过比较可以得出采用模糊控制的干扰观察法可以获得更好的
性能。
4 结 论
鉴于光伏电池的非线性特性,针对光伏发电系统MPPT问题提出了将模糊控制思想应用到最大功率跟踪的控制中,建立了一种基于扰动观察法的模糊控制策略的模型,该模型不需要精确的内部电路特性和相关参数,就可以实现光伏阵列的大功率点跟踪,通过仿真验证了该控制算法在快速性和稳定性方面具有更优的控制性能。
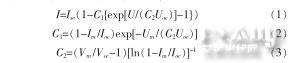
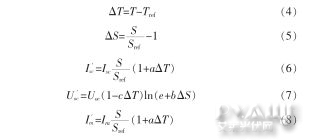







 本届新能源大会以“新城镇、新能源、新生活”为主题,举办2017全球新能源产业峰会及“光伏+”跨界、绿色建筑、分布式市场营销等10场专业论坛,国家能源局新能源和可再生能源司...
本届新能源大会以“新城镇、新能源、新生活”为主题,举办2017全球新能源产业峰会及“光伏+”跨界、绿色建筑、分布式市场营销等10场专业论坛,国家能源局新能源和可再生能源司...














